算法-排列与组合
这篇文章几乎全部是基于对一个非常好的算法讲解仓库的子集排列组合部分进行自己的理解备忘。
对于什么递归回溯概念都知道,之前看了看相关的题目感觉自己会了,然后又忘…………其实就是不会!这次打算对于常用算法的一个长期记录,打算彻底弄明白这些东西!
树
这些问题大多是如何遍历一棵树的问题
排列树
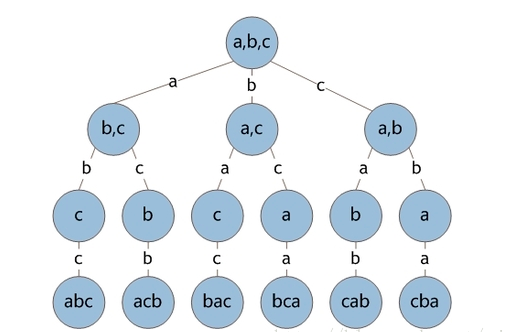 ————-
————-
子集树
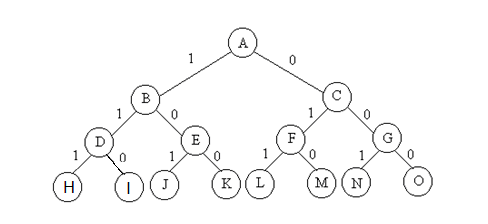
全排列(All Permutation)
给一个 abc 要求输出 abc bac cab acb bca cba。
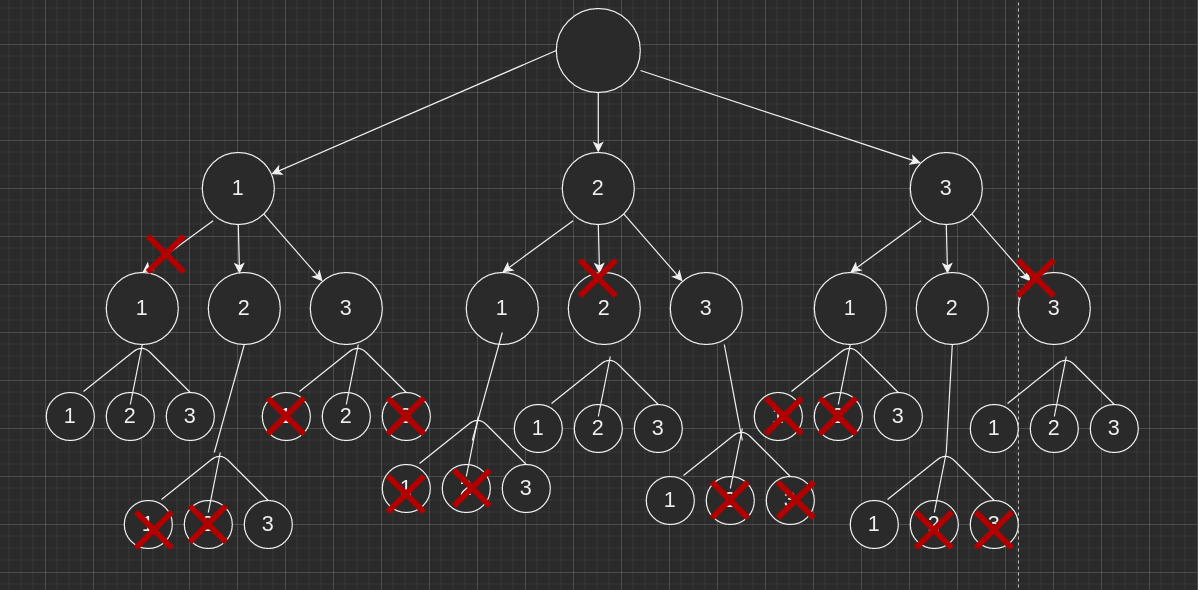
最容易想的就是一个多叉树进行剪枝。 我现在感觉实现一个算法最关键的事情就是如何把你的想法规律化,然后将这个规律转换为相关的代码。关于这个想法,显然也是借鉴别人的……
vector<vector<int>> res;
vector<vector<int>> permute(vector<int> nums)
{
if (nums.size() <=0) return res;
vector<int> track;
backtrack();
return res;
}
void backtrack(vector<int>nums, vector<int> &track)
{
if(track.size() == nums.size()){
res.push_back(track);
return;
}
for(int i=0; i<nums.size(); i++){
if(contains_cpp(track, nums[i])){
track.push_back(nums[i]);
backtrack(nums, track);
track.pop_back();
}
}
}
bool contains_cpp(vector<int> list, int target)
{
for(int i=0; i<list.size(); i++){
if(list[i] == target)
return false;
}
return true;
}
还有一种比较好的办法,使用交换。
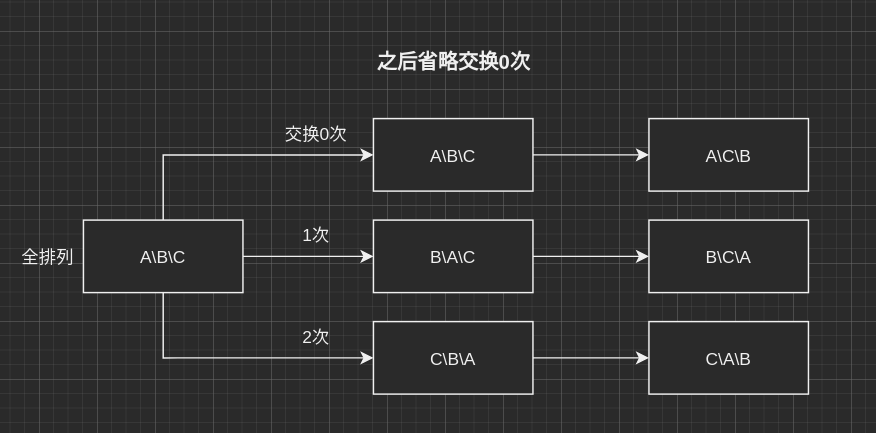
这里面的回溯,之所以要再交换回来的原因就是,其中最后一列的结果需要从上一次的状态进行迁移得到。
void allPermutation(char str[], int from, int to)
{
if(to < 1) return;
if(from == to){
for(int i=0; i<to; i++)
cout << str[i];
cout << endl;
}else{
for(int j=from; j<to; j++){
swap(str[from], str[j]);
allPermutation(str, from+1, to);
swap(str[from], str[j]);
}
}
return;
}
子集(Subset)
输入 nums=[1,2,3] 输出 [ [],[1],[2],[3],[1,3],[2,3],[1,2],[1,2,3] ]
归纳法
具体来说就是,现在让你求 [1,2,3] 的子集,如果你知道了 [1,2] 的子集,在加上 3 就可以了。
vector<vector<int>> subsets(vector<int> &nums)
{
if(nums.empty()) return ;
int back_num = nums.back();
nums.pop_back();
vector<vector<int>> res = subsets(nums);
for(int i=0; i<res.size(); i++){
res.push_back(res[i]);
res.back().push_back(back_num);
}
return res;
}
回溯法
可以发现是树上所有的节点。
vector<vector<int>> res;
vector<vector<int>> subsets(vector<int> &nums)
{
if(nums.empty()) return res;
vector<int> track;
backtrack(nums, 0, track);
return res;
}
void backtrack(vector<int> nums, int start, vector<int>track)
{
res.push_back(tarck); // 先序
for(int i=start; i<nums.size(); i++){
track.push_back(num[i]);
backtrack(nums, start+1, track);
track.pop_back();
}
return ;
}
组合(Combine)
子集和组合之间的区别就是一个需要输出整个树,而另一个由于限制只能输出部分树。
输入 n = 4, k = 2 输出 [ [1,2], [1,3], [1,4], [2,3], [2,4], [3,4] ] 不包含重复的数字。
限制了树的高度以及宽度。
vector<vector<int>> res;
vector<vector<int>> combine(int n, int k){
if(n<=0 || k<=0) return res;
vector<int> track;
backtrack(n, k, 1, track)
return res;
}
void backtrack(int n, int k , int start, vector<int> &track)
{
if(k == track.size()){
res.push_back(track);
return;
}
for(int i=start; i<n; i++){
track.push_back(i);
backtrack(n, k, start+1, track);
track.pop_back();
}
return;
}

